Aquí está la solución al problema de teoría de juegos: "Colaborar es la clave".
Mi metodología de resolución, pasa por codificar las sentendias del problema. Es decir, el resultado de la moneda para Alice y Bob,
Ma = "Lanzamiento de Alice"
Mb = "Lanzamiento de Bob"
y las predicciones de Alice y Bob.
Pa = "Predicción de Alice"
Pb = "Predicción de Bob"
Los valores que pueden tomar las cuatro variables anteriores con cara (C) o cruz (X).
Las posibildades para Ma y Mb , las cuales son aleatorias, se dan en la tabla de la figura 1.
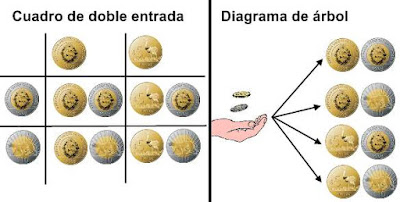 |
| Figura 1: Posibilidades para los lanzamientos de Alice y Bob. |
La clave está en darse cuenta de que primero se lanza la moneda, y después se hace la predicción. Así que las estrategias definidas por Alice y Bob para hacer las previsiones de cada uno sobre el lanzamiento del otro, Pa y Pb, dependerán de lo que pacten Alice y Bob. Pero hay que darse cuenta, que Pa y Pb, pueden usar la información que resulta de su lanzamiento de moneda Ma y Mb.
Primero veamos cuales son las posibilidade de pérdidas. Ambos, Alice y Bob deberán fallar simultáneamente. Codifiquemos las siguientes sentencias:
Fa = "Alice falla en su previsión"
Fb = "Bob falla en su previsión"
Relacionando Fa con Pa y Mb, y Fb con Pb y Ma, tendremos las siguientes equivalencias:
Fa = (Pa = C ^ Mb=X) v (Pa=X ^ Mb=C)
Fb = (Pb = C ^ Ma=X) v (Pb=X ^ Ma=C)
Siendo ^ y v, los operadores lógicos copulativo y disyuntivo respectivamente, es decir, AND y OR.
Por tanto, perder el juego implicaría que: Fa ^ Fb sea cierta
Por el contrario, ganar el juego, sería que
- (Fa = cierta) ^ (Fb = falsa) ,o bien,
- (Fa = falsa) ^ (Fb = cierta) ,o bien,
- (Fa = falsa) ^ (Fb = falsa)
Eligiendo la primera condición de una de las tres sentencias anteriores, se deduce que debe cumplirse los siguiente:
- Desde que Fa es cierta:
- Si Mb = X, entonces Pa = C
- Si Mb = C, entonces Pa = X
- Desde que Fb es falsa:
- Si Ma = X, entonces Pb = X
- Si Ma = C, entonces Pb = C
En forma de tabla es lo siguiente:
Ma = C
|
Ma = X
| |
Mb = C
|
Pa = X y Pb = C
|
Pa = X y Pb = X
|
Mb = X
|
Pa = C y Pb =C
|
Pa = C y Pb = X
|
Desde la anterior tabla, teniendo en cuenta, que para la estrategia Pa, sólo se dispone de Ma, y lo mismo para Pb,
Se puede definir las estrategias siguientes:
- Pa = Ma
- Pb = Nor Mb
La cual permite ganar siempre al juego (-:
La exposición anterior, ha sido bastante forma, pero se entiende que la estreategia que deben seguir Alice y Bob, son para Alice, tomar como previsión el mismo resultado de su moneda, y para Bob, el resultado contrario del lanzamiento de su moneda.
Esto implica que en todos los casos de lanzamientos de Alice y Bob, al menos uno de los dos acertará con su previsión, por tanto ganarán el juego.
No hay comentarios:
Publicar un comentario